Volume of a revolution is a topic generally taught to Year 13 students as part of their Maths or Further Maths A-Level. It used to be in WJEC Core 4 but has now moved to the Further Maths A-Level here in Wales. It’s a juicy topic which brings together graphwork, functions and integration. It also has the ability to surprise – surely one of mathematics’ greatest assets. This post brings together some of the more interesting points of this topic which I hope may be of use to; 1) me so I don’t forget next year! And 2) any teacher who finds themselves teaching volume of a revolution
The Formula
Let’s start with a function f(x) and revolve it around the x-axis. The cross section of this solid, parallel to the y-axis, will be a circle. We can’t sum the volumes of circles but we can use a similar approach by summing the volume of very thin discs. In fact, let’s sum an infinite number of discs of infinite thinness (δx). Let’s start with a disc at a distance of x from the origin.

A small tweak can be made to derive a similar expression that will give the volume of a solid after a rotation of 360° around the y-axis.
Deriving Volume of Sphere & Cone
I like revisiting early mathematical concepts and ideas in order some years later to add layers of depth and understanding. Students learnt the formula for volume of cones and spheres at GCSE but were probably not given the proof. They can practice finding the volume of a revolution by deriving the formula of these two. Here they are:
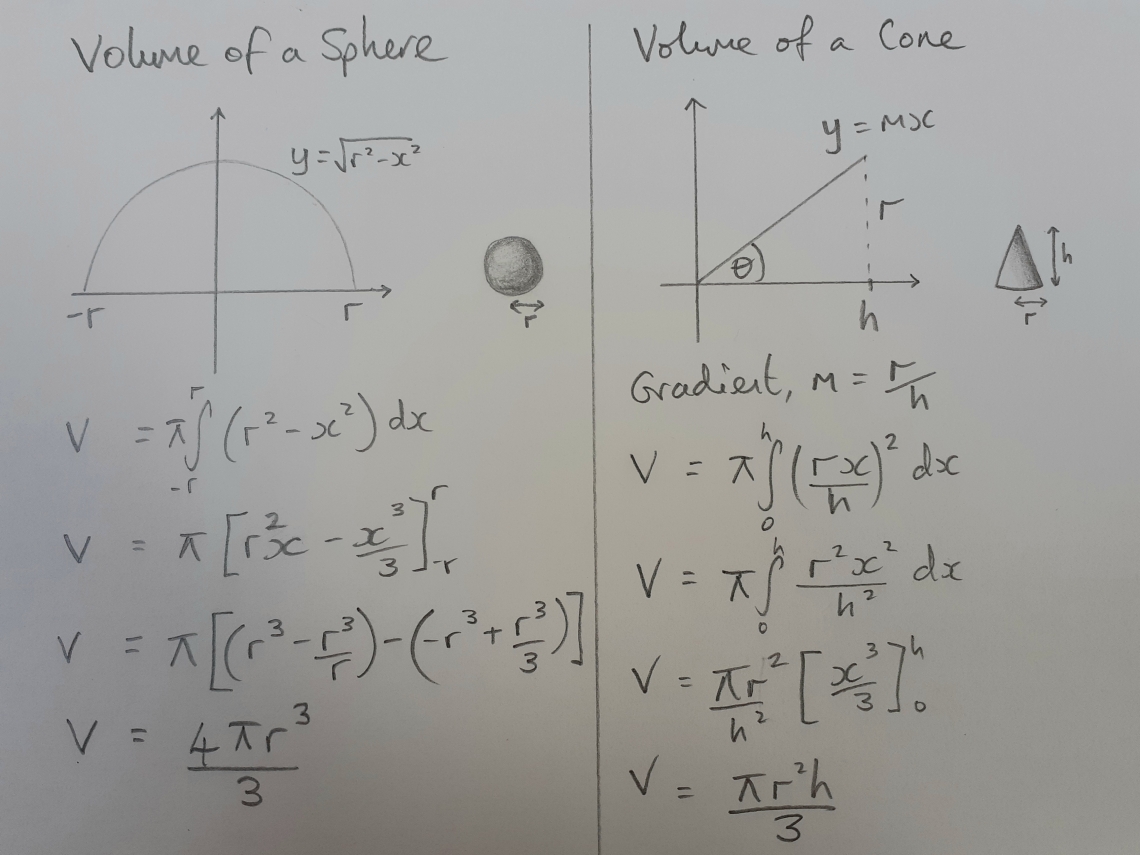
Might be worth making the link here between the volume and the surface area of a sphere (4πr2)
Investigating 1/x and Gabriel’s horn
The curve y=1/x is always good for some investigative work. Consider the part of the curve between x=1 and x=2. Find the volume of the revolved shape when rotated around the y axis (first surprise!) and then compare it to the volume found when rotating it around the x axis (second surprise!).
If we were to find the volume of a revolution of the curve y=1/x rotated around the x-axis, from x=0 to x=∞, we quickly see this cannot be found because of the asymptote as x=0. So if, instead, we set our limits from x=1 to x=∞, we get a volume of π. Bit weird perhaps but OK. However, things get stranger…If we now to calculate the surface area of this horn shape, we find that it is infinite.
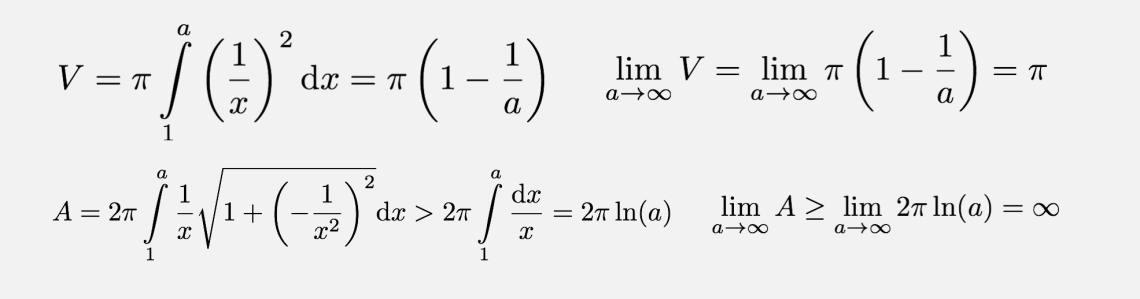
So here we have a 3D object which has a finite volume yet infinite surface area. This, unbeknown to me at the time, is quite a well known curiosity known as Gabriel’s Horn. There’s quite a bit in the wiki page to impress and bamboozle your students with – from the painter’s paradox to trying to find an object with finite surface area yet infinite volume.
As always, any questions or comments most welcome.
Thanks to mathcentre.ac.uk for the graphic.


There is a lovely activity on this here:
Click to access gabriel.pdf
Print out the coloured sheets and students can make their own Gabriel’s horn.
LikeLike