I have never been particularly happy about the way I teach factorising non-monic quadratics (quadratics where the coefficient of x2 is greater than 1). My students can follow the method I use but often forget it in tests and assessments and don’t really understand the mechanics behind it. Inspired by Jo Morgan’s new book, A Compendium of Mathematical Methods, our maths department explored six methods of factorising non-monics. We did this at a recent department meeting. I have described the method briefly for each technique as I solve the same quadratic: 6x2 – 5x – 4, with some comments. We also voted as a department on our favourite method to teach – results are at the end.
Splitting the middle term
- Find two numbers that multiply to make ac and add to make b. So here we are looking for two numbers that multiply to make -24 and add to make -5. Those two numbers are -8 and 3
- Split the middle (coefficient of x) term into two terms. So -5x is re-written as -8x + 3x. The -8x and 3x can be written in any order
- Factorise the first two terms, and factorise the 3rd and 4th The terms in the brackets should be equal to each other
- Factorise again by considering how many of the term in the bracket you have. In this example we have (2x + 1) lots of (3x – 4)

This is the method I was taught as a student and the one I’ve promoted most in my 10 years of teaching (how often is that the case?!). It’s probably the most widely taught method amongst our department. It is quite straightforward but does need students to remember the steps. It’s not clear why the splitting of the middle term has to done in the given way. Also, the step 3 to 4 isn’t natural for students if they haven’t practised factorising expressions in the form of a(x + y) + b(x + y).
Non-monic to monic
- Label the quadratic as y so we can follow what we will be doing…
- Multiply both sides by the coefficient of x2, in this case 6
- Re-write the RHS as a quadratic in terms of ax, in this case 6x
- Make a substitution in order to exemplify that what we have now is a monic quadratic
- Factorise this monic using two numbers that multiply to make -24 and add to make -5
- Substitute the 6x back in place of A
- Factor out the HCF of both brackets
- Divide both sides by 6 (or whatever your a was) to complete the factorisation

I like this method. I had not seen it before reading Jo Morgan’s book but it makes a lot of sense. It isn’t the quickest and I probably wouldn’t use it when factorising quadratics myself, but I can imagine teaching it. There are links to be made here with disguised quadratics that students will meet in Year 12. Note that we wouldn’t have had to multiply through by 6 is the first term was already a perfect square, such as a 9x2 or 25x2. However, as I was presenting this method, I sensed that departmental colleagues thought it/I was overcomplicating the whole thing!
Lyszkowski/Howell’s Method
- Write two brackets with each beginning with ax, in this case 6x
- Find the two numbers that multiply to make -24 and add to make -5, so this is -8 and 3
- Place each of these numbers in the brackets as shown (in any order) and divide by a
- Factorise both brackets by taking out the HCF. This/These factor(s) will be equal to the divisor so divide both numerator and denominator by this (i.e. cancel)
- Factorisation will be complete

I first heard of this method from a colleague who heard it from a student at a local school called Howell’s (hence our school’s name for it!). That colleague, @MissAyresCHS, presented this method to the department as her preferred method. The ‘Lyszkowski’ refers to Richard Lyszkowski who published the method is a mathematical journal in 1999. At first glance I didn’t like it because the first step seemed alien. However, having seen the non-monic to monic method (above) it makes more mathematical sense as it’s just that method but without some of the steps. The omission of steps does speed up the process but does arguably take away some of the understanding.
By Inspection
- Consider factor pairs of a and c (ignoring the signs for now)
- Try different combinations of differences between products of a factor of a and a factor of c. Or, simply write out different combinations and start eliminating ones that don’t work
- Once you’ve found the correct numbers, figure out the signs using trial and error or experience!
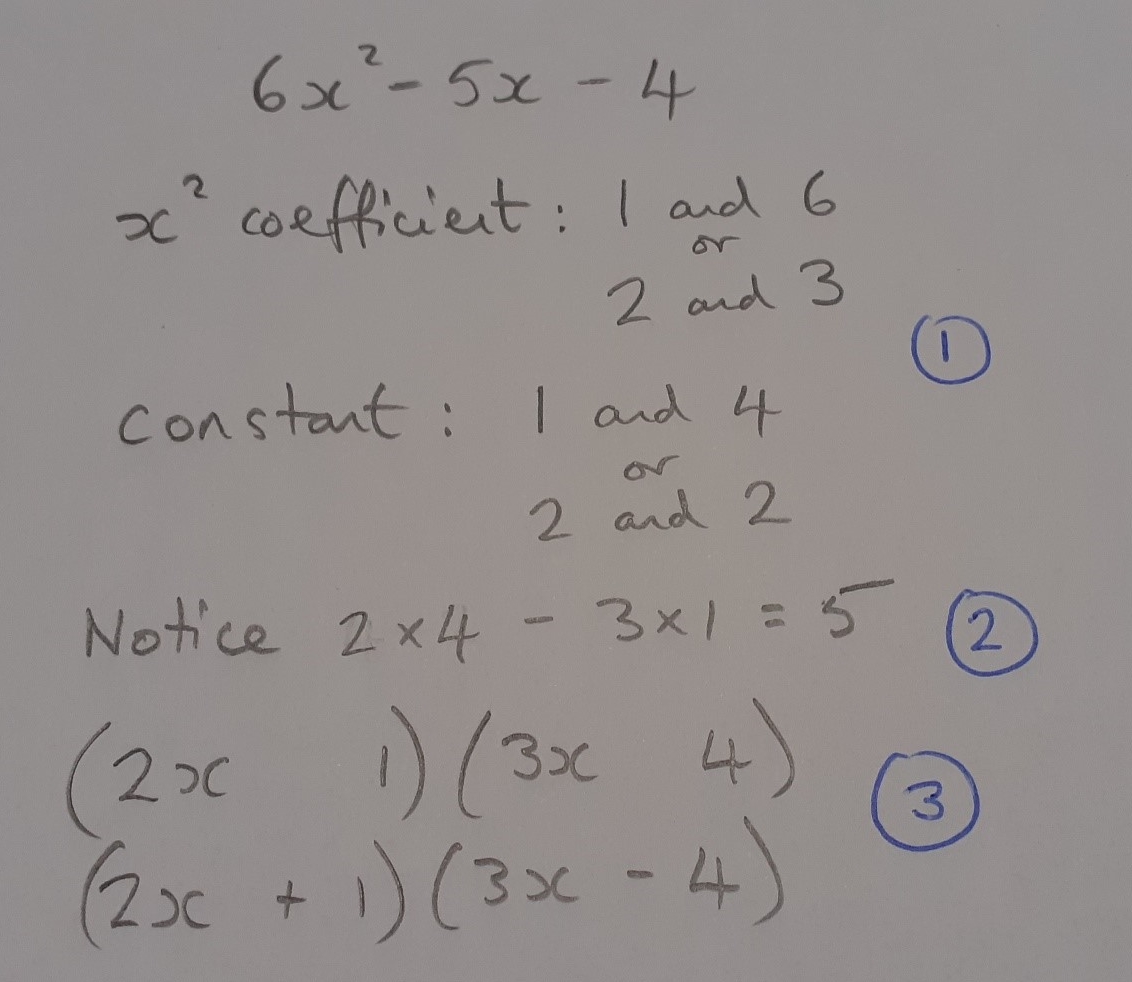
This method was presented to the department by @DevonaldMr who is a big inspection fan since he was taught it as a student himself. If you are good at this method, it is the most efficient and quickest way to factorise a non-monic quadratic. It doesn’t require any memorisation of steps and no reasoning/proof is required to see why it works. However, it is difficult if a and/or c have lots of factors and I’ve found that most students simply don’t like trying to spot it and prefer using a reliable method instead. Personally, I would use this method for easier examples, but I have never managed to get good enough to use it for all quadratics. I asked my Yr12 & Yr13 further mathematicians their preference and about 75% of them said that they use inspection to factorise all quadratics.
Magic X
- Write a large X and place ac in the top section and b at the bottom. Find the two numbers that multiply to make -24 and add to make -5, so this is -8 and 3. These go on the left and right of the X in any order
- Divide both the -8 and 3 by a, the coefficient of x2
- Simplify the fractions you now have
Write a pair of brackets and use the denominators as the coefficient of x and the numerators as the constant terms

This method is very quick. It can be done in just one X and the results pops out surprisingly quickly. I had never seen it until recently and I think it’s based on a Vedic method. The speed and efficiency comes at a price as the method doesn’t promote mathematical understanding. Proving why it works would be a worthwhile diversion, one that I haven’t tried myself yet. I admire its efficiency but would probably be reluctant to teach this method as it goes against our department’s philosophy of promoting mathematical understanding.
Grid Method
- Knowing that the quadratic can be factorised as a product of two linear terms, draw a 2×2 grid
- Place two x’s on the outside of the grid as shown and then put the term in x2 in the top left box and the constant term in the bottom right
- Find the two numbers that multiply to make -24 and add to make -5, so this is -8 and 3. Place these in the two empty boxes in any order as coefficients of x
- Factor out the HCF of the two rows to find 3x and -4. Use a similar approach to the columns, or deduce what needs to be written on top of the grid given what you already know
- Gather your factors and write in a pair of brackets to complete the factorisation

I hadn’t seen this approach before, but I really like it. You still have to ‘split the middle term’ but it shows more of what you’re doing that the first method described above. The grid links well with earlier work with area and multiplying pairs of brackets, as well as at AS level where the department’s preferred method of teaching polynomial division is by using a grid.
Department’s View
At the department meeting, following the presentation of the methods, colleagues used some of the different approaches to factorise other quadratics and much discussion followed. The magic X method was very divisive with the debate centred around speed vs understanding. The inspection method was also quite divisive with that debate centred around what we do in our own maths versus what we teach our students. We discussed having a common departmental approach but this was not well received because we different methods would suit different students (and teachers!). Several colleagues were pleased to understand some of the methods that students were using that they have picked up from outside of school from tutors, youtube etc.
In order to gauge the preferred methods of colleagues, I gave everyone 5 counters and asked them to distribute them as they wish between the 6 methods. The results are below.

The grid method was the overwhelming winner with twice the number of votes as splitting the middle term in second place. I placed 4 of my counters for the grid method so I was pleased to see I had backed a winner! I saved one counter for inspection as I do think there’s a place for inspection with easier quadratics as students gain fluency. Poor non-monic to monic received no votes – I think the length of the process put people off. It will be interesting to see how students respond to some of these methods which are new to us. We will be revisiting the topic at a department meeting later in the year for some feedback as of course it will be interesting to see what the students think!
Any comments or questions more than welcomed.

